Cauchy Priors Redux

 Victor Chernozhukov posed the following question on twitter a few days ago:  "Suppose that X~ N(0,1), and Y ~ Cauchy, X and Y are independent. What is   E[X | X+Y]?"

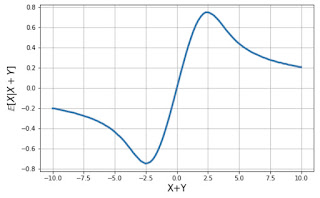
Thien An replied "isn't it the mean of the density proportional to exp(-x^2/2)/[1+(z-x)^2]?" and she included this nice plot

illustrating the behavior of E(X | X+Y).

This recalled some rather ancient suggestions by Jim Berger about the utility of Cauchy priors.Reformulating Victor's question slightly, suppose that X ~ N(t,1) and you have prior t ~ C, Thien's nice plot can be interpreted as showing the posterior mean of t as a function of X. For small values of |X| there is moderate shrinkage back to 0, and as |X| grows the posterior mean does too.  However, for large values of X, this tendency is reversed and eventually very large |X| values are ignored  entirely.  This might seem odd, why is the data being ignored?

I like to think about this in terms of the comedian Richard Pryor's famous question:  "Who are you going to believe, me, or your lying eyes*."  If the observed X is far from the center of the prior distribution, you decide that it is just an aberration that is totally consistent with your prior belief that t could be quite extreme since the prior has such heavy tails, but you stick with your prior belief that it is much more likely that t is near 0.

In contrast if  the prior were Gaussian, say, t ~ N(0,1),  then the posterior mean is determined by linear shrinkage, so E(t|X) is midway between 0 and X, and for large |X|, we end up with a posterior mean in a place where neither the prior or likelihood have any mass.

* In this case "me" should be interpreted as your prior, and X as what you see with your lying eyes.

Convexification and Potato Peeling

 You may have wondered, as I have, about the convexifying effect of peeling a potato, so it comes as a great relief that this is a well studied subject.  The opening paragraph of Goodman (1981) is priceless:

A swivel-type potato peeler, when used in the usual (and somewhat wasteful) way, produces a convex peeled potato, which is a subset of the original unpeeled and non-convex potato. This suggests, in an obvious way, the problem of maximizing the volume of a convex body contained in a given non-convex body. That such a largest convex subset exists follows at once from the Blaschke selection theorem (see Proposition 1 below). The problems then become: (1) What proportion of the original volume are we assured of saving? and (2) How do we determine the largest convex 'peeled potato' inside a given non-convex one ?

A swivel-type potato peeler, when used in the usual (and somewhat wasteful) way, produces a convex peeled potato, which is a subset of the original unpeeled and non-convex potato. This suggests, in an obvious way, the problem of maximizing the volume of a convex body contained in a given non-convex body. That such a largest convex subset exists follows at once from the Blaschke selection theorem (see Proposition 1 below). The problems then become: (1) What proportion of the original volume are we assured of saving? and (2) How do we determine the largest convex 'peeled potato' inside a given non-convex one ?

A swivel-type potato peeler, when used in the usual (and somewhat wasteful) way, produces a convex peeled potato, which is a subset of the original unpeeled and non-convex potato. This suggests, in an obvious way, the problem of maximizing the volume of a convex body contained in a given non-convex body. That such a largest convex subset exists follows at once from the Blaschke selection theorem (see Proposition 1 below). The problems then become: (1) What proportion of the original volume are we assured of saving? and (2) How do we determine the largest convex 'peeled potato' inside a given non-convex one ?A swivel-type potato peeler, when used in the usual (and somewhat wasteful) way, produces a convex peeled potato, which is a subset of the original unpeeled and non-convex potato. This suggests, in an obvious way, the problem of maximizing the volume of a convex body contained in a given non-convex body. That such a largest convex subset exists follows at once from the Blaschke selection theorem (see Proposition 1 below). The problems then become: (1) What proportion of the original volume are we assured of saving? and (2) How do we determine the largest convex 'peeled potato' inside a given non-convex one ?A swivel-type potato peeler, when used in the usual (and somewhat wasteful) way, produces a convex peeled potato, which is a subset of the original unpeeled and non-convex potato. This suggests, in an obvious way, the problem of maximizing the volume of a convex body contained in a given non-convex body. That such a largest convex subset exists follows at once from the Blaschke selection theorem (see Proposition 1 below). The problems then become: (1) What proportion of the original volume are we assured of saving? and (2) How do we determine the largest convex 'peeled potato' inside a given non-convex one ?