Cauchy Priors Redux

 Victor Chernozhukov posed the following question on twitter a few days ago:  "Suppose that X~ N(0,1), and Y ~ Cauchy, X and Y are independent. What is   E[X | X+Y]?"

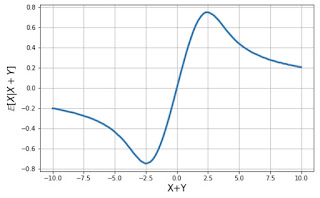
Thien An replied "isn't it the mean of the density proportional to exp(-x^2/2)/[1+(z-x)^2]?" and she included this nice plot

illustrating the behavior of E(X | X+Y).

This recalled some rather ancient suggestions by Jim Berger about the utility of Cauchy priors.Reformulating Victor's question slightly, suppose that X ~ N(t,1) and you have prior t ~ C, Thien's nice plot can be interpreted as showing the posterior mean of t as a function of X. For small values of |X| there is moderate shrinkage back to 0, and as |X| grows the posterior mean does too.  However, for large values of X, this tendency is reversed and eventually very large |X| values are ignored  entirely.  This might seem odd, why is the data being ignored?

I like to think about this in terms of the comedian Richard Pryor's famous question:  "Who are you going to believe, me, or your lying eyes*."  If the observed X is far from the center of the prior distribution, you decide that it is just an aberration that is totally consistent with your prior belief that t could be quite extreme since the prior has such heavy tails, but you stick with your prior belief that it is much more likely that t is near 0.

In contrast if  the prior were Gaussian, say, t ~ N(0,1),  then the posterior mean is determined by linear shrinkage, so E(t|X) is midway between 0 and X, and for large |X|, we end up with a posterior mean in a place where neither the prior or likelihood have any mass.

* In this case "me" should be interpreted as your prior, and X as what you see with your lying eyes.

Convexification and Potato Peeling

 You may have wondered, as I have, about the convexifying effect of peeling a potato, so it comes as a great relief that this is a well studied subject.  The opening paragraph of Goodman (1981) is priceless:

A swivel-type potato peeler, when used in the usual (and somewhat wasteful) way, produces a convex peeled potato, which is a subset of the original unpeeled and non-convex potato. This suggests, in an obvious way, the problem of maximizing the volume of a convex body contained in a given non-convex body. That such a largest convex subset exists follows at once from the Blaschke selection theorem (see Proposition 1 below). The problems then become: (1) What proportion of the original volume are we assured of saving? and (2) How do we determine the largest convex 'peeled potato' inside a given non-convex one ?

A swivel-type potato peeler, when used in the usual (and somewhat wasteful) way, produces a convex peeled potato, which is a subset of the original unpeeled and non-convex potato. This suggests, in an obvious way, the problem of maximizing the volume of a convex body contained in a given non-convex body. That such a largest convex subset exists follows at once from the Blaschke selection theorem (see Proposition 1 below). The problems then become: (1) What proportion of the original volume are we assured of saving? and (2) How do we determine the largest convex 'peeled potato' inside a given non-convex one ?

A swivel-type potato peeler, when used in the usual (and somewhat wasteful) way, produces a convex peeled potato, which is a subset of the original unpeeled and non-convex potato. This suggests, in an obvious way, the problem of maximizing the volume of a convex body contained in a given non-convex body. That such a largest convex subset exists follows at once from the Blaschke selection theorem (see Proposition 1 below). The problems then become: (1) What proportion of the original volume are we assured of saving? and (2) How do we determine the largest convex 'peeled potato' inside a given non-convex one ?A swivel-type potato peeler, when used in the usual (and somewhat wasteful) way, produces a convex peeled potato, which is a subset of the original unpeeled and non-convex potato. This suggests, in an obvious way, the problem of maximizing the volume of a convex body contained in a given non-convex body. That such a largest convex subset exists follows at once from the Blaschke selection theorem (see Proposition 1 below). The problems then become: (1) What proportion of the original volume are we assured of saving? and (2) How do we determine the largest convex 'peeled potato' inside a given non-convex one ?A swivel-type potato peeler, when used in the usual (and somewhat wasteful) way, produces a convex peeled potato, which is a subset of the original unpeeled and non-convex potato. This suggests, in an obvious way, the problem of maximizing the volume of a convex body contained in a given non-convex body. That such a largest convex subset exists follows at once from the Blaschke selection theorem (see Proposition 1 below). The problems then become: (1) What proportion of the original volume are we assured of saving? and (2) How do we determine the largest convex 'peeled potato' inside a given non-convex one ?

Two new vinaigrettes

 I've added two new vinaigrettes to the growing list at http://www.econ.uiuc.edu/~roger/research/vinaigrettes/vinaigrette.html

One is a survey of currently available methods for estimation and inference for quantile regression, the other is about computational methods for univariate quantiles.  Both incorporate some new methods in my quantreg package.  As usual there is an element of samo-kritika  to these notes, since they try to reflect several drawbacks of the current state of affairs, not just the successes.

Economics of Writing

 I've been wondering lately about the economics of writing since I find myself spending quite a lot of time writing open source software and writing about open source software.  There seem to be two extreme positions on this subject:

    o  Ben Smith quotes the Substack author Heather Cox Richardson as saying, "if you start doing things for money, they stop being authentic."

    o  Or there is Samuel Johnson:  "No man, but a blockhead ever wrote, except for money."

A Chicago price theory question might be:  Reconcile these two statements.

Conformal Quantile Regression

 I've written yet another vinaigrette, this time about a simple R implementation of the conformal quantile regression method introduced by Romano, Patterson and Candes  the pdf version of the vinaigrette is available here.

There, there

The LRB is distributing a daily serving of "greatest hits" from their back issues, articles that  made a big impression on readers and/or the editors.  Yesterday's article was part 1 of Derek Parfit's piece
"on the universe" which struck me as steaming pile of metaphysical nonsense.  It prompted the
following questions, with apologies to Gertrude Stein:

Why is there no there there?
Why is there there there?

Reason vs Rationality

The Gelman Blog mentioned a paper by Lorraine Daston called The Moral Economy

of Science, [Osiris, Vol. 10, Constructing Knowledge in the History of Science

(1995), pp. 2-24] which attracted my attention because long ago I read E.P.

Thompson's The Moral Economy of the English Crowd [Past & Present

No. 50 (Feb., 1971), pp. 76-136] that made an extremely persuasive case for

delicate balance between the legitimacy of the rural market for agricultural

goods and riots when this legitimacy falls apart.  Thompson prefaces his paper

with the passage from Proverbs:  "He that withholdeth Corn, the People shall

curse him: but Blessing shall be upon the Head of him that selleth it."

Daston is at pains to distinguish her thesis from Thompson's -- she is not

about the legitimacy of science in the broader culture/environment, but the

argument, which is more about the moral economy within the scientific

community, is nonetheless quite appealing.  As such departures from one's

usual reading sometimes do, this led me done a rabbit hole of related

reading concluding with a video lecture by Daston from 2010 called "Rule

of Rules:  Or how Reason became Rationality", which constitutes a cogent

historical survey of the rise of algorithms as a substitute for judgement

and reason.  Since post WWII economics has bought into the algorithmic,

mechanistic decision making zeitgeist with a vengeance, Daston's lecture

is a refreshing antidote to the familiar brainwashing of the discipline.

As I joked when I forwarded the link of the lecture to an old friend, "I'm

not sure whether the lecture is better than "Marriage Italian Style", the

last movie I've watched, but I'm working on an algorithm to decide this."

Daston has a book with Peter Galison (he of How Experiments End) on

"Objectivity", which I've not yet read, but surely must contain the following

quotation that also appears in Daston's Moral Economy paper:

    Goethe gave voice to the worries that impel mechanical objectivity when he

    preached caution in interpreting experimental results: "For here at this pass,

    this transition from empirical evidence to judgment, cognition to application,

    all the inner enemies of man lie in wait: imagination, which sweeps him away  

    on its wings before he knows his feet have left the ground; impatience; haste;

    self-satisfaction; rigidity; formalistic thought; prejudice; ease; frivolity;

    fickleness -- this whole throng and its retinue. Here they lie in ambush and

    surprise not only the active observer but also the contemplative one who

    appears safe from all passion." Johann Wolfgang Goethe, "The Experiment as

    Mediator between Object and Subject" (1792, publ. 1823)

Coincidentally, the latest Economist letters column contains related passage

from the "melancholy finale of Giuseppe Tomasi di Lampedusa’s novel, The Leopard

    Nowhere has truth such a short life as in Sicily; a fact has scarcely happened five

    minutes before its genuine kernel has vanished, been camouflaged, embellished,

    disfigured, squashed, annihilated by imagination and self interest; shame, fear,

    generosity, malice, opportunism, charity, all the passions, good as well as evil,

    fling themselves onto the fact and tear it to pieces; very soon it has vanished

    altogether

Sicily is now faced with some stiff competition in this domain.